Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=a căn 2 (Miễn phí)

Câu hỏi:

14/01/2020 159,602

Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=a $\sqrt{2}$ . Số đo góc thân thuộc hai tuyến đường trực tiếp AB và SC bằng ?

Trả lời:

Giải vì chưng Vietjack

Đáp án là B

Cách 1. Xác toan và tính góc thân thuộc hai tuyến đường trực tiếp.

Tam giác ABC vuông bên trên A

Do SA=SB=SC nên nếu như gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đàng tròn trĩnh nước ngoài tiếp tam giác ABC mà tam giác ABC vuông bên trên A nên H là trung điểm của BC.

Dựng hình bình hành ABCD. Khi đó:(AB,SC)=(CD,SC) và CD=AB=a. Tam giác SBC vuông bên trên S

có SH là đàng trùng tuyến nên SH= $\frac{a \sqrt{2}}{2}$

Tam giác CDH có

theo toan lý Cô- Sin tớ có

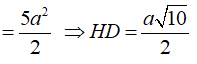
Tam giác SHD vuông bên trên H nên

Tam giác SCD có:

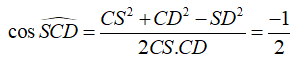
Cách 2. (Hay phù phù hợp với bài bác này) Ứng dụng tích vô phía.

Theo fake thiết có

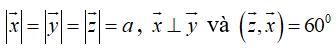
Ta có

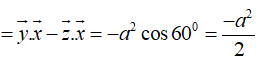
Suy ra:

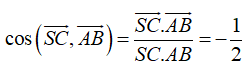
Nhà sách VIETJACK:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tính thể tích khối chóp S.ABC có AB=a, AC=2a, $\hat{B A C} = 120^{O}$ , SA $⊥$ (ABC), góc thân thuộc (SBC) và (ABC) là $60^{O}$ .

A. $\frac{\sqrt{7} a^{3}}{14}$

B. $\frac{3 \sqrt{21} a^{3}}{14}$

C. $\frac{\sqrt{21} a^{3}}{14}$

D. $\frac{\sqrt{7} a^{3}}{7}$

Câu 2:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA=SC, SB=SD. Trong các khẳng định sau, khẳng định nào đúng ?

A. $S A ⊥ (A B C D)$

B. $S O ⊥ (A B C D)$

C. $S C ⊥ (A B C D)$

D. $S B ⊥ (A B C D)$

Câu 3:

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OB=OC=a $\sqrt{6}$ , OA=a, . Khi cơ góc thân thuộc nhị mặt mũi phẳng lặng (ABC) và (OBC) bằng

A. $30^{o}$

B. $90^{o}$

C. $45^{o}$

D. $60^{o}$

Câu 4:

Hình chóp S.ABCD có đáy ABCD là hình vuông vắn cạnh a, hình chiếu vuông góc của S trên mặt mũi phẳng lặng (ABCD) trùng với trung điểm của AD, M là trung điểm của CD cạnh mặt mũi SB hợp với lòng một góc $60^{o}$ . Thể tích của khối chóp S.AMB là

A. $\frac{a^{3} \sqrt{15}}{6}$

B. $\frac{a^{3} \sqrt{15}}{12}$

C. $\frac{a^{3} \sqrt{15}}{3}$

D. $\frac{a^{3} \sqrt{15}}{4}$

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CD, BC, SA. H là phú điểm của AC và MN. Giao điểm của SO với (MNK) là điểm E. Hãy chọn lựa cách xác lập điểm E đúng nhất nhập tư phương án sau:

A. E là phú của MN với SO.

B. E là phú của KN với SO.

C. E là phú của KH với SO.

D. E là phú của KM với SO

Câu 6:

Cho hình tứ diện ABCD có toàn bộ những cạnh bằng 6a. Gọi M,N lần lượt là trung điểm của CA, CB. P là điểm bên trên cạnh BD sao cho tới BP=2PD. Diện tích thiết diện của tứ diện ABCD bị tách vì chưng (MNP) là

A. $S = \frac{5 a^{2} \sqrt{147}}{2}$

B. $S = \frac{5 a^{2} \sqrt{147}}{4}$

C. $S = \frac{5 a^{2} \sqrt{51}}{2}$

D. $S = \frac{5 a^{2} \sqrt{51}}{4}$

Bình luận

Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi phản hồi

Bình luận